因果推断简介

作者个人理解：

因果推断本质上回答的问题：谁是因？谁是果？这个因会导致多大的果？抽象为两大问题即为：因果发现+因果效应估计。对应到我们日常的业务策略、产品迭代中，因（某个策略、ui改版、产品迭代）会导致多大的果（点击率提升多少？笔数提升多少），回答这类“干预”问题的黄金准则是随机控制实验（Randomized Control Trial），这一点已成为当今自然科学家和社会科学家的共识。但是日常中，我们很多的策略/产品的效果是无法设计完美的随机实验的，这就要求我们从观察性数据中去（拟合随机试验）发现因果关系、测算因果效应。

利用因果推断，从观察数据中去计算因果效应（从混杂因子角度去拆分）主要可以分为两类方法：

1. 不能有未被观察到的混杂因素：通俗来讲，我们需要知道所有可能影响 “果”的因素，这类方法包括PSM（propensity score method，倾向性得分匹配法）、CEM（Coarsened Exact Matching，广义精确匹配）、DID（Difference in Differences，双重差分模型）、SCM（Synthetic Control Methods，合成控制法），Uplift model（实质上是ITE的估计，Individual treatment effect ，个体的因果效应)、RRD（Regression Discontinuity Design，断点回归）等。本文第二节将简要介绍这些方法的原理和适用场景，实战可见-参考文献-推荐阅读。
2. 可以有未被观察到的混杂因素：这类方法可以在数据有未被观察到（unobserved /hidden confounder）的情况下使用，所以这类方法非常吸引人，工具变量也就是这类方法。目前ATA上对这部分的讨论也较少，本文也将在第三节 基于对 Causal Inference: What If[1] 的学习，展开对因果推断中工具变量的讨论。

效应估计的常用方法

不能有未被观察到的混杂因素：通俗来讲，我们需要知道所有可能影响 “果”的因素，这类方法包括 匹配类方法（PSM、CEM、IPTW、DID、合成控制法）、Uplift Models、断点回归等。其中：

• 倾向性得分匹配（PSM，Propensity Score Method）：主要是基于用户特征来预测用户被活动干预的概率作为倾向得分，选取和实验组用户倾向得分最接近的用户作为对照组；“倾向性得分” 是一个用户属于实验组的 “倾向性”，理论上，如果我们对每一个实验组用户都在对照组里匹配一个得分相等的用户，就能得到同质的实验组和对照组，进而来做组间比较。“倾向性得分匹配” 适用于样本属性的维度很高或者有一些（不好切断的）连续变量，为实验组找到匹配的对照组，消除混杂因子[2]。

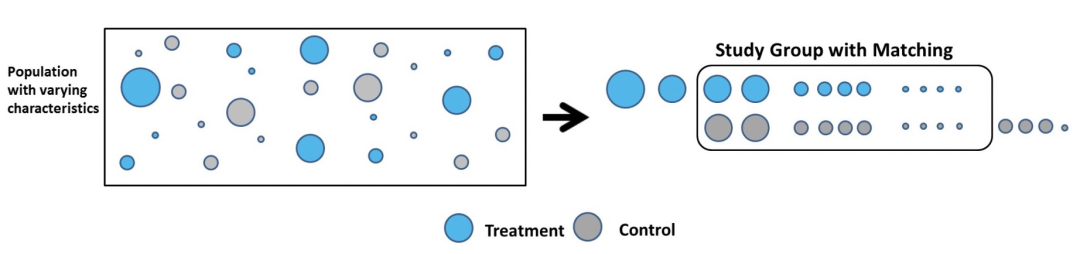
• 广义精确匹配（CEM，Coarsened Exact Matching）：主要是使用核心混杂因子（对“果”/“因变量” 影响较大的用户特征）进行匹配，每个实验用户匹配到的N个同特征用户作为对照组，取N个同特征用户的核心指标均值作为实验用户的对照。CEM主要用于用户量特别大的场景，在这种情况下预测倾向得分依赖于大量的计算资源和较优的模型效果，导致PSM会受到一定的影响。
• 逆策略概率加权（IPTW，Inverse Probability of Treatment Weighting）：基于PSM，对策略效果进行加权计算，通俗来讲，就是样本越倾向选择这个策略，那么说明这个策略对该样本可能获得更好的策略效果，所以取逆得到的权重来平衡这个策略效果[3,4]。
• 双重差分模型（DID，Difference in Differences）：本质是寻找自然对照组，是政策效果评估中常用的一种计量识别策略，原理是基于反事实框架来评估政策发生（e.g. A市开通高铁，实验组）和不发生（e.g. 与A市近似同质、且未开通高铁的B市，对照组）这两种情景下因变量（e.g. GDP增长）的变化。
• 合成控制法（SCM，Synthetic Control Methods）：基于DID，基本思想是，我们通常很难找到与A市完全相似的B市，但通常可对若干大城市进行适当的线性组合，以构造一个更为优秀的“合成控制地区” (synthetic control region)，并将“真实A市”与“合成A市”进行对比，故名“合成控制法”。合成控制法能够克服在选取对照对象时出现的样本选择偏误以及政策内生性问题。使用这个方法的一个关键点在于选择好最优权重矩阵，使得合成的对照组与实验组在treatment前的情况高度类似[5]。
• Uplift model：Uplift即为增益，Uplift models 主要用于预测一个treatment（e.g. 发优惠券）对个体（e.g. 给某个消费者）的增量价值（e.g. 这个消费者购买概率的提升值），实质上是因果推断中对ITE（Individual treatment effect ）个体的因果效应的估计，常用于机器学习领域。

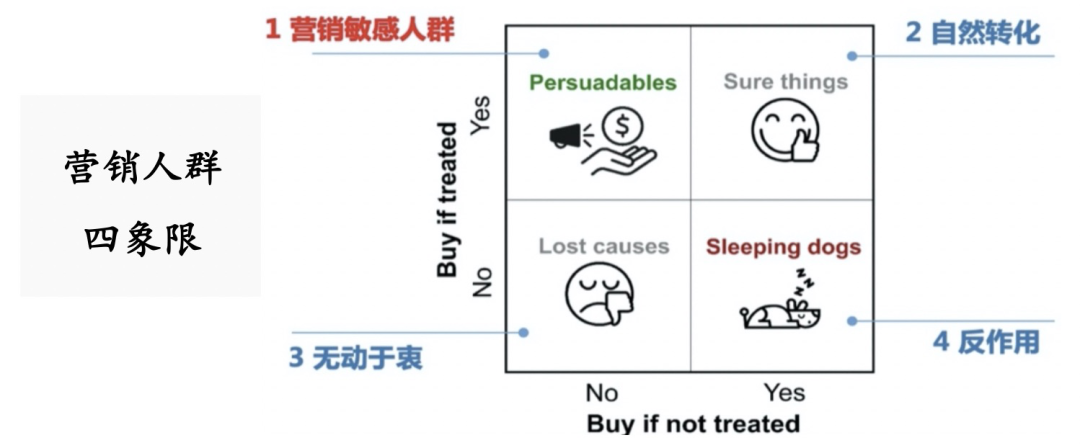
• 断点回归（RDD，Regression Discontinuity Design）：基本思想是存在一个连续变量, 该变量能决定个体在某一临界点两侧接受政策干预的概率，由于X在该临界点两侧是连续的，因此个体针对X的取值落入该临界点任意一侧是随机发生的，即不存在人为操控使得个体落入某一侧的概率更大，则在临界值附近构成了一个准自然实验[6]。学术界普遍认为断点回归的设计更接近准自然实验, 估计的结果更加准确。

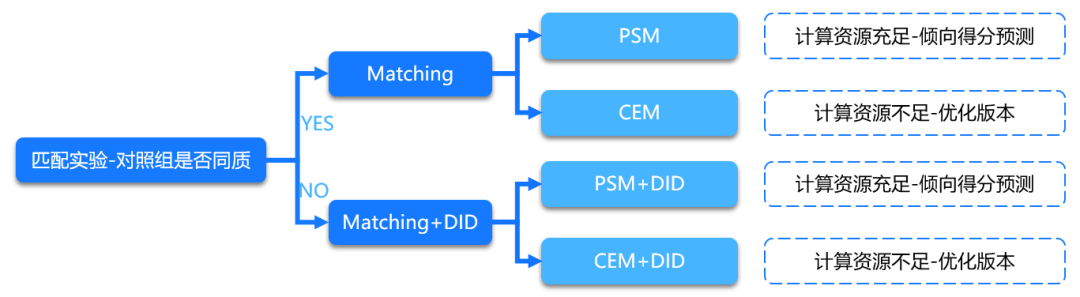
应用在实际的业务效果/增量衡量中时，对于匹配类方法，在匹配得到同质的实验 vs 对照组的情况下，活动带来的业务效果即为活动开始后实验组和对照组的核心指标差值（Matching）。而当在通过以上匹配类方法没能找到完全同质的实验 vs 对照组的情况下，可依据匹配到的实验组和对照组用户，再结合DID的方法来去除干预前两组之间的GAP，通过匹配+DID类方法来计算因果效应（Matching+DID）。

工具变量介绍

对于工具变量，学习过计量经济学的同学应该非常熟悉，其实因果中的工具变量和计量中常说的工具变量本质上是一个东西，那么工具变量 (Instrumental variables) 的在效应估计的作用到底是什么？参考某知乎答主的对其在计量ols估计中的回答： “过滤器，把X 中和 随机扰动项 相关的部分过滤掉，只剩下正交的部分，这样OLS就又重振雄风了。工具变量就是这个过滤器。” [7]

工具变量的三个条件

下图3.1 描绘了一项双盲随机试验， Z 是被试的分组情况(1:治疗组，0:安慰剂组)， A 是被试的实际接受治疗情况(1:实际上接受治疗，0:实际上未接受治疗)，Y 是结局，U 是所有能影响结局和被试配合程度的未测变量。

如果我们想一致地估计 A对Y 的因果效应均值（ATE），那不管使用什么方法，我们都需要测量U（可以把U理解为控制变量）， 并在我们的模型中调整U，由于U是未测的，所以这些方法只能得到有偏的估计。 但工具变量方法却并不一样，即使我们不能测量并调整U ，我们依然可以用这一方法去估计 A 对 Y 的效应均值。

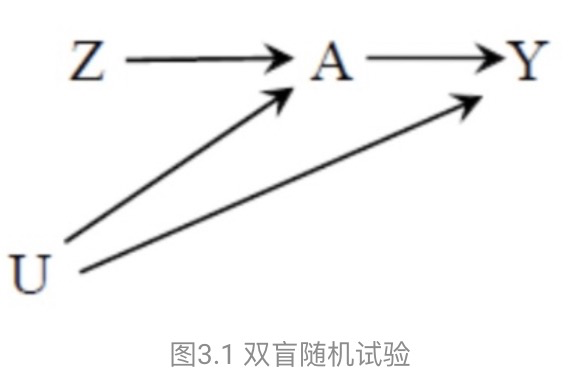
那么对于工具变量 Z ，它需要满足以下三个条件: (1) Z 和 A 相关；(2) Z 仅通过 A 影响Y，而不能直接影响Y；(3) Z 和 Y 没有共同诱因。对于图上这个双盲随机试验中， Z 就是一个工具变量。 我们逐个来看三个条件：Z (1) 被分配到治疗组的被试更可能接受治疗，满足Z 和 A 相关，(2) 这是一个双盲设计，满足Z 仅通过 A 影响Y，而不能直接影响Y，(3)治疗组的分配是随机的，不受任何其他因素影响，满足Z 和 Y 没有共同诱因。并且，在图 2.1 中，工具变量 Z 对实际治疗 A 有因果效应，我们将 Z 称作因果性工具变量。

在What if的前几章，作者用不同的方法在观察性数据中估计了戒烟对增重的因果效应。为了使用工具变量估计因果效应，我们需要一个工具变量 Z 。然而观察性研究并不像随机试验一样有一个表示随机分组的变量，所以我们需要使用其他变量作为我们的工具变量，其中一个可能选项是香烟的价格。香烟价格似乎能满足工具变量的三个条件：(1)香烟价格能影响一个人是否戒烟；(2) 香烟价格只通过戒烟与否对体重产生影响；(3)香烟价格和增重之间没有共同诱因。

现在我们有了香烟价格Z这个变量，并把它用在我们接下来的讨论当中。假设Z =1表示研究参与人员所在州的香烟均价高于 1.5 美元， Z = 0 表示其他情况。不过，我们依然不能判定 Z 是否是一个工具变量。在工具变量的三个条件中，只有(1)是可验证的，此时我们只需证明 Z 和A相关，也即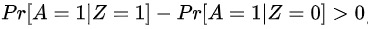。Z =1时有25.8%的人戒烟；Z =0时有 19.5%的人戒烟。因而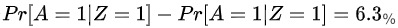。在我们的例子中，Z 和A微弱相关，此时Z 被称为弱工具变量。

然而，我们不能验证条件(2)和(3)。为了验证条件(2)，我们需要证明 Z 只通过 A 影响 Y。但如果存在Uz，就可能存在一条对撞路径 Z <- Uz -> A <- U ->Y，此时控制 A 就会使得 Z 和Y 相关，也就不能用这一方法验证条件(2)。同样，我们也不能验证条件(3)，因为我们没有办法知道效应估计中是否存在混杂。我们只能假设(2)和(3)成立。因此，工具变量这一方法和其他方法一样，需要依赖于一些不可验证的假设。

(有些时候，我们能够利用数据证伪(2)和(3)，然而，证伪只能通过验证假设中的一小部分不成立从而拒绝假设，并不具备效力说明假设中的大部分是否不成立。)

在观察性研究中，我们不能证明我们认为的工具变量 Z 是否是真正的工具变量，所以我们将 Z 称为候选工具变量。我们能做的，就是利用各专业知识说明候选变量 Z 为什么能满足条件 (2)和(3) 。这就如同前几章我们用专业知识为我们的模型假设辩护一样。 ---先验知识/业务经验的重要性。

工具变量的效应估计

如果 Z 满足工具变量的三个条件(以及一个额外条件，我们将在下一小节讨论)，并且是一个二分变量，那么在加法尺度上，工具变量的效应估计就可以表示为:

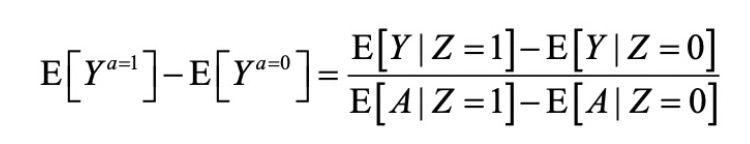
为了直观地理解这一表达式，我们可以再思考一下上一小节中的随机试验。这个表达式中的：

1. 等式左边：是A对Y的效应
2. 等式右边-分子：是 Z 对 Y 的效应，也被称为治疗意向效应，Z 是工具变量，Y是“果”
3. 等式右边-分母：是 Z 对 A 的效应，表示被试的配合程度，Z是工具变量，A是“因”

如果被试完全配合研究人员，那么分母就等于1， A 对 Y 的效应就等于 Z 对 Y 的效应（完美的随机实验）。如果配合程度不佳，那么分母就会趋近于 0（小于1），从而有 A 对Y 的效应大于 Z 对 Y 的效应。不配合的被试越多，这两个效应之间的差距也就越大。 这一效应估计不需要调整任何混杂，而是通过给治疗意向效应乘以一个膨胀系数得到。被试的配合程度越低，也即 Z -A 之间的关系越接近于 0，那膨胀系数也就越大，在观察性研究中同理。

所以，使用工具变量时，我们需要对这一表达式分子和分母中的效应进行估计。在我们戒烟的例子中，工具变量 Z 是一个二分变量(1:参与人员所在州的香烟均价高于 1.5 美元，0:其他)。

1. 分子的估计值是
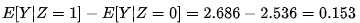
2. 而分母的估计值为
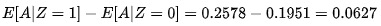
3. 因而可以得到治疗效应的估计值是 0.153 / 0.0627 = 2.4 kg

在工具变量的三个条件以及第四个附加条件之下，2.4kg就是戒烟对增重的因果效应均值 (这一方法也被称为 Wald 估计法) 。

除了Wald估计法以外，我们也可以用双阶最小二乘法拟合两个(饱和)线性模型从而估计表达式中的分 子和分母（需要作出很强的参数假设），也可以使用结构模型（避开强假设）、然后通过G-估算 计算结构模型中的某些参数。在工具变量中到底是使用二阶最小二乘法还是使用结构模型， 就类似于在没有工具变量的时候到底是使用结局回归还是结构嵌入模型一样，各有利弊。

不过无论如何，本小节介绍的表达式如果要被认为是治疗 A 对结局 Y 的因果效应均值，那我们需要工具变量的第四个条件成立。接下来，我们将讨论第四个条件。

工具变量的第四个条件

同质性

本小节中工具变量的三个条件1-3不足以保证工具变量的效应估计，就是治疗 A 对 Y 的因果效应。除此之外，我们需要第四个条件：(4)效应的同质性。本小节，我们将讨论 (4)的不同形式以及它在学术历史中的发展变化。

1. 完全同质：最极端也是最古老的同质性被表述为：治疗 A 对结局 Y 的效应对每个人来说都是相等且不变的。 例如，如果戒烟让每个人都增加同样的体重(比如 2.4kg)，那么就符合完全同质，因果效应就是2.4kg这一常数，然而这在现实中几乎是不可能的。在戒烟的例子中，戒烟会让有的人增重许多、让有的人增重一 点、甚至让有的人体重变轻。
2. 加法尺度上的同质性：在1)不够实际的情况下，同质性后来被放宽为第二种形式，对二分变量 Z ，治疗组或非治疗组中 A 对 Y 的效应在 Z 的每一个分层中相等，即如下公式，不过这是加法尺度上的同质性，即。
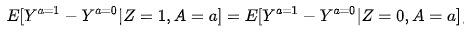
3. 在未测混杂因素中A对Y 的因果效应同质：A对Y 的因果效应在未测混杂U 的每一分层中都相等，如下公式，然而这个假设依然是不可验证的，且不太可信，因为未测混杂很可能就是效应修饰因子。比如戒烟对增重的影响很可能就因吸烟频率的不同而不同，同时吸烟频率自身也是一个混杂因素，即。
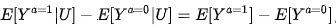
4. 另一种形式的同质性，在加法尺度上Z-A的相关性，在未测混杂因素U 的不同分层中不变。

不过，因为同质性在许多场合中都显得不合理，所以许多研究者对能否使用工具变量得到有效的效应估计抱持怀疑态度，不过我们还有其他两种方法能让我们避开同质性条件。 其中一种方法是在工具变量的模型中包含研究起始时的变量。如此一来，我们就能放宽双阶最小二乘法中的参数假设，也就能更放心地使用工具变量。在模型中包含初始变量会限制治疗在 协变量各分层中的变化情况，同时允许治疗组中的因果效应随 Z 而变化 (也就是加入初始变量，使两组“处理后”的用户符合同质性条件) 。

另一种方法是放弃同质性，使用另一个条件(4)。新的条件(4)虽然不足以让我们估计人群中的因果效应均值，但将会让我们工具变量的效应估计有因果性意义。我们将在下一小节讨论 另一种条件4。

单调性

让我们再回到最开始的双盲随机试验，其中有表示治疗分组的变量 Z 、表示实际治疗情况的 变量A、以及表示结局的变量Y。对于试验中的每一名被试，我们将反事实变量定义为这名 被试被分配到治疗组( z =1)时他的实际治疗情况，同理。 如果我们知道每个被试的和，那我们就可以将所有被试分为互不重叠的四组:

1. 都会接受治疗，即被试不管有没有被分配到治疗组，都接受治疗，即。
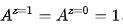2. 都不会接受治疗，即被试不管有没有被分配到治疗组，都不接受治疗，即。
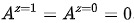3. 配合者，即被试实际治疗情况总会和他们的分组相同，即。
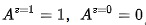4. 对抗者。即被试实际治疗情况总会和他们的分组相反，即。

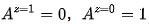如果不存在对抗者，那单调性成立，这是因为工具变量 Z 的取值变大，要 么A 不变、要么也导致 A 的取值变大 (配合者)。只有对对抗者来说， Z 取值变大会导致 A 取值变小。或者换句话说，如果对所有人有 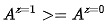，那么单调性成立。

现在我们将上一小节中的同质性替换为单调性，让单调性成为我们的第四个条件。那么工具变量的效应估计就不再是 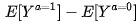。在单调性下，工具变量的效应估计等于配合者中的因果效应均值，也即。

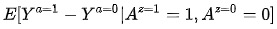简单而言，工具变量的效应估计的分子，也即 Z 对 Y 的因果效应，就等于本小节四个不同分组中 Z 的效应的加权平均。然而，在都会接受治疗与都不会接受治疗这两组中， Z 对 Y 的效应为0，这是因为 Z 对 Y 的因果效应需要通过 A ，而 A 的取值 在这两组中是固定的。同时，在单调性条件下，不存在对抗者。因此，工具变量的效应估计的分子，就是配合者中 Z 对 Y 的因果效应——也就是配合者中 A 对 Y 的因果效应——再乘以配合者所占的比例。而配合者所占的比例，就等价于工具变量的效应估计中的分母。

(配合者中的因果效应均值是一个子群体中的因果效应，可能与整个人群的因果效应不尽相同。)

在观察性研究中，如果不存在对抗者，我们就可以通过工具变量估计配合者中的治疗效应。 然而严格而言，在观察性研究中不存在配合者或对抗者，这是因为观察性研究中没有治疗分配， 也就不存在配合或不配合。在我们戒烟的例子中，配合者指的是住在香烟价格高的州就戒烟、而 住在香烟价格低的州就不戒烟的人。与之相反，对抗者指的是住在香烟价格高的州就不戒烟、而 住在香烟价格低的州就戒烟的人。如果不存在对抗者且因果性工具变量是二分变量，那么 2.4kg 就是配合者中的效应估计。

在 1990 年代，用单调性替代同质性被视为工具变量方法的救星。主要是因为同质性在大多数情形中并不可信，而单调性则更可信。不过，单调性假设下的工具变量也有很多缺点：

1. 单调性假设下的工具变量不能估计整个人群的因果效应，而只能估计配合者中的因果效应（类似CATE，Conditional Average Treatment Effect）。
2. 其次，在观察性研究中，单调性假设也并非总是成立。
3. 最后，将人群根据配合程度分成四组这一做法可能并不合理（在许多现实情景中，配合者是劣定的）。

(Deaton等在2010年的paper中这样评价配合者中的效应:“这偏离了我们的初衷。原本光线很强，能照耀各个角落。但现在我们控制了光线能照射的地方，然后宣称这就是我们一直以来希望看到的东西。”)

总而言之，如果我们只关心配合者中的因果效应，那在只涉及两个分组的双盲随机试验中， 单调性就是一个合适的假设。然而，当情形更加复杂或涉及观察性研究，即使我们的工具变量是真正的因果性工具变量，我们也需要倍加小心。

再谈工具变量的三个条件

工具变量三个条件的剖析

前两个小节我们讨论了同质性或单调性作为工具变量第四个条件的优劣。我们的讨论都假设了Z 是一个有效的工具变量。然而在观察性研究中，Z 可能并不满足工具变量三个条件中的 (2)和(3)，因而就不是一个有效的工具变量；也可能 Z 仅仅勉强满足(1)，那么Z 就只是一个弱工具变量。在这两种情况中，就算条件(4)完美成立，使用工具变量也会导致很强的偏移。现在，我们再详细讨论一下每个条件：

条件(1)：Z 和 A 相关。

这一条件可以实证地验证。研究者在使用工具变量之前，需要先验证 Z 和 A 是否相关。然而，就像我们戒烟例子中一样，如果 Z 和 A 之间的相关性很弱，那就是一个弱工具变量，这可能带来三个严重的问题:

1. 弱工具变量会导致 95%置信区间变宽。
2. 弱工具变量会放大因条件(2)和(3) 不成立带来的偏移。 Z 和A 的弱相关性会使得工具变量效应估计中的分母变小，而条件(2)和 (3)影响的是分子，如果分子有偏移，那么这一偏移将会被放大。在我们戒烟的例子中，任何分子中的偏移都会被乘以 15.9(1/0.0627)。
3. 即使样本够大，弱工具变量也会带来偏移，并导致效应估计方差的低估。也即，效应估计是错误的，且置信区间太窄了。

条件(2)：Z 仅通过A 影响Y ，而不能直接影响Y 。

在因果图中，如果有箭头从 Z 指向 Y ，那就违反了条件(2)，就如图 3.4.1 所示。这一箭头不经过治疗 A ，因而将会直接作用于工具变量效应估计的分子，而这一额外部分也会被视为 A 的效应的一部分，从而被分母扩大。在图3.4.2中，条件(2)对原变量 A 成立，但对于A*并不成立，这是因为 路径 Z → A → Y 所表示的 Z 的效应并没有经过 A*，而我们估计的却是 A的效应。在实践中，为了简便，很多时候我们只能用近似的 A*（如上文提到的香烟价格是否>=1.5）替代真实的 A，这种近似替代是工具变量的一个主要问题。

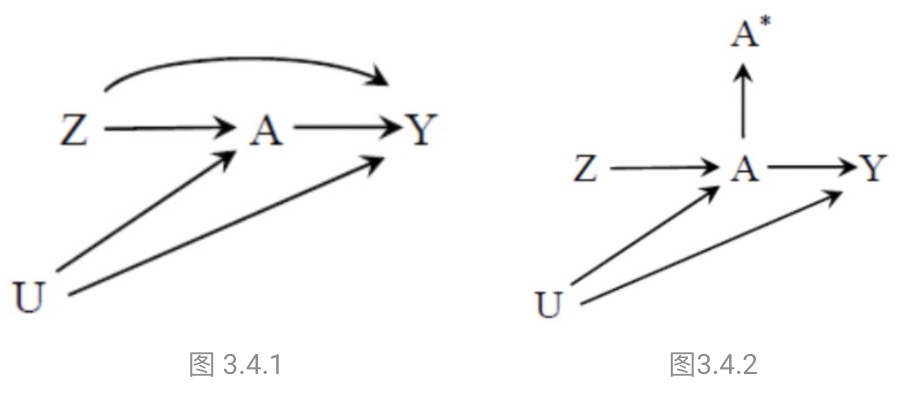
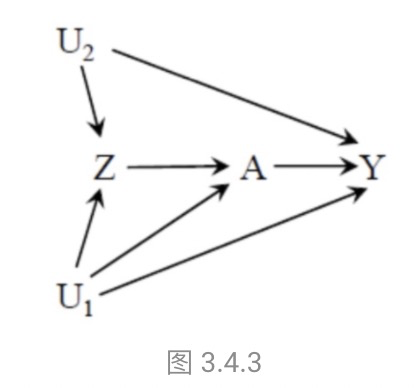
条件(3)：Z 和 Y 没有共同诱因。

这一条件同样无法验证。图3.4.3 描绘了 Z 和 Y 存在共同诱因的情形，其中U1不仅是Z和Y的共同诱因，也是 A 的诱因。在观察性研究中，Z 的混杂总是存在（对于其他研究者不能控制的变量也同理）。而混杂会影响效应估计里面的分子，同时也会被视为 A 的效应的一部分，从而被分母扩大。

一些对和不对的解决方法

1. 部分解决办法：利用在分层中假设3成立的方法进行验证：某些时候，条件(3)和其他条件在某些变量的分层中更可能成立。相比于直接假设 Z 和 Y 之 间没有混杂，加上“在变量V 的分层中”这一限制可能会更好一些，也即假设“在某些变量V 的 分层中， Z 和Y 之间没有混杂”。从而我们就可以在V 的分层中利用工具变量估计因果效应，然后再假设治疗的因果效应在整个人群(同质性)或者配合者(单调性)中是不变的，进而汇总这些分层中的效应估计。
2. 不对的方法：用已测混杂在不同分层的分布“预测”在未测混杂中的分布： 研究者也经常检验工具变量Z 的不同分层中已测混杂的分布，从而为条件(3)提供支撑。 这一做法是基于这样一种想法：如果已测的变量已经分布均衡了，那未测变量同样分布均衡的可能性会高一些。然而，这一想法可能会造成致命的错误，这是因为即使再小的不均衡，经过(前文讨论的)放大之后，也会造成很大的偏移。多个工具变量可能加剧效应估计的偏移：有些研究者会同时使用多个工具变量，从而缓和只有一个工具变量的不足。然而使用多个工具变量会加剧我们上述讨论的种种问题。工具变量的数目越多，它们中的某些也就越可能违反工 具变量的三个基本条件。

工具变量与其他方法比较

工具变量和我们前面讨论的（需要识别出所有混杂因子的）方法至少在三个方面不同：

1. 就算数据是无限的，工具变量也需要模型假设，而此时逆概率加权与标准化不需要。 如果我们有人群中每个人的治疗、结局、以及混杂数据，我们就能用非参数化的逆概率加权和标准化两种方法估计治疗的因果效应均值。而在工具变量中，我们仍然需要模型去估计治疗的因果效应。在数学上，同质性等价于将结构模型中的所有乘积项参数设定为 0，也就是说，工具变量方法不存非参数的形式(工具变量不是唯一没有非参数形式的方法，断点回归分析等方法也没有非参数形式) 。
2. 稍微违反条件(1)至(4)会造成不可预测的极大偏移。工具变量的一个理论基础是效应估计中的分母会扩大分子中的效应。因此，当这些条件不成立的时候，或者是一个弱工具变量的时候，就可能导致不可预测的极大偏移。工具变量的效应估计对假设条件的变化非常敏感，这一特质使得工具变量对于圈外人来说是一种非常危险的方法，同时也再一次强调了敏感性分析的重要性(Baiocchi等在他们2014年的论文中讨论了量化工具变量敏感性的方法) 。
3. 能使用工具变量的理想情形相较于其他方法来说更不常见。我们讨论过，工具变量主要用于有大量未测混杂、有一个二分变量A 、以及有一个很强的因果性工具变量 Z 的情形之中，同时还需要同质性/或单调性成立。这些限制使得工具变量只能用于简单的因果推断情形当中，比如比较 A = 1 与 A = 0 的效应。

总结

本文对因果推断中效应估计的各类方法进行了介绍，主要包括对 需要识别出所有混杂因子 的PSM、CEM、IPTW、DID、SCM、Uplift model、RDD等方法的简单介绍，以及对 不需要识别出所有混杂因子 的工具变量方法的深入讨论。因果推断依赖于假设的明确性，以及对各种假设的详细剖析。工具变量所需的假设和其他方法不同，因而成为一种吸引人的新方法。然而，因为工具变量对假设的要求非常严格，所以使用工具变量的时候，我们需要对它的种种限制保持警惕（虽然这一提醒对所有因果推断方法都适用）。期待因果效应的估计在我们的讨论之后，有更多的同学能一起参与学习与研究、迎得更好的发展~~

参考文献

1. Causal Inference: What If
2. 数据分析 36 计（9）：倾向得分匹配法 (PSM) 量化评估效果分析，PSM
3. A Survey on Causal Inference，IPTW/IPW
4. 因果推断文献解析|A Survey on Causal Inference(3)，IPTW/IPW
5. 合成控制法 (SCM): 只有一个实验对象的政策评价，SCM
6. Instruments, Randomization, and Learning about Development
7. 断点回归（regression discontinuity design）学习笔记 ，RDD
8. 工具变量 (Instrumental variables) 的作用到底是什么？，IVTutorial in Biostatistics: Instrumental Variable Methods for Causal Inference，IV