
该文章主要介绍倾向得分匹配(PSM, Propensity Score Matching)方法的原理以及实现。这是一种理论稍微复杂、但实现较为容易的分析方法,适合非算法同学的使用。可用于(基于观察数据的)AB实验、增量模型搭建等领域。
文章主要分为四部分:前置知识(因果推断)介绍、倾向得分计算与匹配与匹配质量检验、匹配示例与增量计算还有一些补充的小知识点。对因果推断有简单了解的同学可以跳过第一部分,直接从第二节开始阅读。
前置知识介绍
对因果推断概念有所了解或想直接学习PSM的同学可跳过这一节。
概念一:干预效果 Treatment Effect
干预效果(Treatment Effect):干预下的潜在结果减去未干预时的潜在结果(Rubin框架),即:
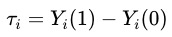
其中 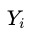 表示潜在结果,1和0代表是否受到干预。
表示潜在结果,1和0代表是否受到干预。
- 举个例子:我们想知道我养狗给我提升了多少幸福度,理想情况下就是用我养狗时的幸福度减去我不养狗时的幸福度。
概念二:ATT Average Treatment Effect on the Treated
相较于个人的干预效果,我们更希望了解人群整体的干预效果,毕竟我们通常用策略干预的是一个人群。
应用PSM,我们通常希望计算得到被干预的用户的平均干预效果,即ATT(average treatment effect on the treated),即
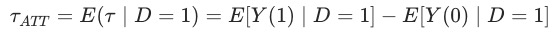
其中变量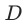 代表是否收到干预。
代表是否收到干预。
可以看到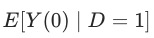 代表被干预的用户假如不被干预的情况下的潜在结果,是一个无法观测的数值。倘若可以建立AB测试,我们可以利用对照组得到该结果,在无法进行AB测试的情况(例如
代表被干预的用户假如不被干预的情况下的潜在结果,是一个无法观测的数值。倘若可以建立AB测试,我们可以利用对照组得到该结果,在无法进行AB测试的情况(例如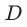 是一个主动的行为)我们可以通过PSM拟合一个虚拟的对照组进行计算。
是一个主动的行为)我们可以通过PSM拟合一个虚拟的对照组进行计算。
计算ATT所需满足的假设
这里引入一个新的概念,倾向性得分(Propensity Score),即用户受到(参与)干预的概率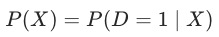
- 条件独立假设 CIA (Conditonal Independence Assumption)
给定一系列可观测的协变量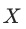 ,潜在结果和干预分配相互独立。
,潜在结果和干预分配相互独立。
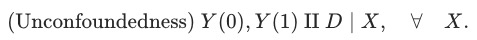
可认为所有影响到干预分配与潜在结果的变量都同时被观测到。此时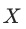 可能是高维度的。
可能是高维度的。
若上式成立,则干预分配与潜在结果基于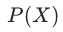 同样条件独立[可证明],即:
同样条件独立[可证明],即:
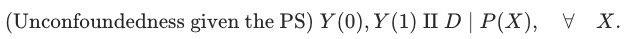
- 共支撑 Common Support
在一些文献中,该条件也被称为strong ignotability.
除了独立外的另一个条件是存在重叠的部分,即:
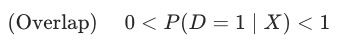
这个条件能够排除掉——给定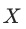 时能准确确定
时能准确确定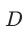 的情况(也因为如此才有匹配的空间)。
的情况(也因为如此才有匹配的空间)。
估算ATT
在满足CIA和common support的情况下,我们能够对ATT进行估算:
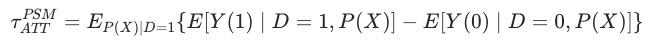
即:在common support 上,以倾向分为权重、对实验组与对照组平均值的差值进行求和。
PSM实现
倾向得分匹配的实现步骤其实就如其名称中提到的,主要有两步:倾向得分的计算,以及基于倾向得分的匹配。
倾向得分预测
预测用户被干预的概率,其实就是一个常见的二分类问题,常见的机器学习模型都可以在这里使用。
特征选择
需要注意的是在特征选择上,具体需要哪些特征呢?有两个基本的原则是需要遵守的:
- 同时影响干预分配和结果的变量应该被包括(使CIA成立);
- 被干预项影响的变量应该排除(变量需要在干预项前计算)。
而至于特征的量级,不同的文献中有不同的说法:
- 不应使用过多的参数,因为会导致如下两个问题:
- 恶化support问题,导致存在某些
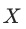 使得
使得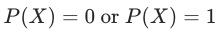
- 不会增加bias但会增加variance,因为匹配困难一些treatment样本会被丢弃、或control样本被重复使用
- 尽可能使用更多的参数以满足CIA假设,除非有明确的共识特征与干预无关。
为方便起见,通常在实际应用中我们会选取尽量多的特征,同时也会用到一些机器学习中常规的特征筛选方法。
重要特征
当我们已知一些特征十分重要(对干预、结果)时,我们可能通过一些方式加强这些特征对匹配的影响:
- 在匹配时在该特征上两组一致,如男性只跟男性匹配
- 在子人群中做匹配(男性、女性分别做匹配)
换句话说:就是在重要特征上做完全匹配,再辅助倾向分匹配(当预期在不同分组上会有不同的ATT时尤其推荐这么做)。
匹配算法
当不使用propensity score时,可以直接基于协变量进行匹配,直接计算两个样本协变量之间的(马氏距离(Mahalanobis Distance) - 知乎 (zhihu.com)),这种方式通常称为CVM(Coviate Matching)。
完成倾向分模型及预测后,每个样本会得到一个propensity score,此时便可以进行匹配步骤了:为每个被干预的样本匹配一个(或多个)虚拟的对照样本。
匹配的基础思路很简单,即找到一个距离最近的样本,实现的具体方法按照渐进的顺序阐述如下:
Nearest Neighbour Matching 最近邻匹配
这是最直接的一种方法,即:对干预组中的用户,选取对照组中在倾向分上相差最小的用户做匹配。
实现上,会有有放回和无放回两种实现方式:
- 有放回(对照组样本可重复使用):此时整体匹配质量上升,bias下降,当干预组与对照组倾向分分布差异较大时推荐应用。此时使用的对照组样本数会减少,导致variance上升;
- 无放回:此时匹配结果与匹配顺序有关,顺序需要保证随机。
除了是否放回之外,还有一个可调整的地方在于对单个用户是否可匹配多个样本(over-sampling):通过匹配最近的多个邻居降低了variance,提升了匹配的稳定性。但此时需要给每个邻居赋予权重(eg. 按距离衰减)。
Caliper and Radius Matching 有边界限制的半径匹配
当最近的邻居也相距很远的时候,NN匹配会存在低质匹配的风险。很自然的,我们想到可以限定样本间分数差值的上限,即Caliper。
- Caliper Matching:匹配时引入倾向分差值的忍受度,高于忍受度的样本丢弃。理论上通过避免低质量匹配降低了bias,但在样本数量较少时也可能因为匹配过少而升高了variance;
- Radius Matching:不止匹配caliper中的最近样本,使用caliper中的所有样本进行匹配。这种方法的优势在于,当有高质量匹配时使用了更多的样本、而当缺乏高质量匹配时则使用较少的样本。
Stratification and Interval Matching 分层区间匹配
分层匹配可以看作radius matching的一种相似版本,即将倾向得分分成多个区间,在每个区间内进行匹配。需要注意的是,分层的依据除了propensity score,也可以用一些我们认为重要的特征(如性别、地区),在相同特征的用户间进行匹配。
匹配示例SQL
在计算复杂度不太高的情况下,我们通常能够使用sql进行匹配算法的实现,示例如下:
with matching_detail as (
select t1.user_id as treatment_userid,
t1.score as treatment_pscore,
t2.user_id as control_userid,
t2.score as control_pscore,
row_number() over (partition by t1.user_id order by abs(t1.score-t2.score) asc) as rn
from propensity_score_treatment t1
left join propensity_score_control t2
-- 分层匹配
on t1.gender = t2.gender and round(t1.score, 1)*10 = round(t2.score, 1)*10
where abs(t1.score-t2.score) <= 0.05 -- caliper matching
)
select * from matching_detail where rn = 1 # rn大于1时为多邻居/radius匹配上述的三种方法实际上都只使用了对照组中的部分样本,若希望使用对照组中的所有样本可对对照组中的样本整体赋权,计算整体的差值。
匹配质量检验
鉴于我们基于倾向分做匹配,需要检测其他特征在实验组与对照组之间的分布是否相近。
理论依据:因为 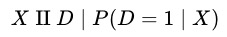 ,在给定
,在给定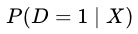 的情况下,
的情况下,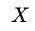 与
与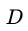 应该相互独立。也就是说倾向得分相同时,
应该相互独立。也就是说倾向得分相同时,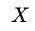 的分布应该趋近一致。
的分布应该趋近一致。
- 可量化的指标——标准化偏差 Standardised Bias
通过标准化偏差我们可以衡量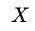 在实验组与对照组分布的差异大小,通常我们认为低于5%的偏差是可以接受的(当然越小越好)。
在实验组与对照组分布的差异大小,通常我们认为低于5%的偏差是可以接受的(当然越小越好)。
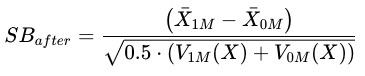
我们也可以在匹配前后分别计算该值,去看看通过匹配让Standardised Bias减少了多少。
- 对样本均值的假设检验——T检验
我们也可以通过双侧T检验去判断两组的变量均值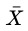 是否有显著差异。缺点是匹配前后偏差的减少量无法很直观的感受到。进一步的,我们也可以基于倾向分先做一个分层,再进行T-Test。这样可以看到不同分值下匹配的质量。
是否有显著差异。缺点是匹配前后偏差的减少量无法很直观的感受到。进一步的,我们也可以基于倾向分先做一个分层,再进行T-Test。这样可以看到不同分值下匹配的质量。
- 联合显著性/伪
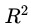
另一种思路是我们把特征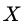 当作自变量,是否干预当作因变量,计算判定系数
当作自变量,是否干预当作因变量,计算判定系数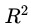 。在完成匹配后,两组间的协变量
。在完成匹配后,两组间的协变量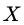 应该不存在系统性差异(即无法通过
应该不存在系统性差异(即无法通过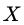 预测是否干预),从而
预测是否干预),从而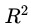 应该很低。类似的,可以对所有变量做一个联合F-Test,匹配有效的话,匹配后会拒绝假设(即解释变量对被解释变量的共同影响不显著)。
应该很低。类似的,可以对所有变量做一个联合F-Test,匹配有效的话,匹配后会拒绝假设(即解释变量对被解释变量的共同影响不显著)。
除此之外,我们可以通过QQplot的可视化、计算匹配后两组方差的比值、计算匹配前后倾向分偏差减小量等方式衡量匹配质量。但总体来说还是推荐前两种方式——计算SB和T检验,兼具了可解释性和可量化性。假如匹配的质量达不到要求,那么我们就要回到上一步对匹配算法进行调整。
匹配结果+增量计算
示例数据均为虚拟构造数据,仅用于参考说明方法。
匹配结果示例
匹配之后,常见的趋势会如下图一所示:
- 在干预之前,匹配后的实验组和对照组呈现几乎相同或平行的趋势(匹配质量较好的情况下)
- 在干预后,两组用户在目标指标上会开始出现差异,可以认为是干预带来的影响
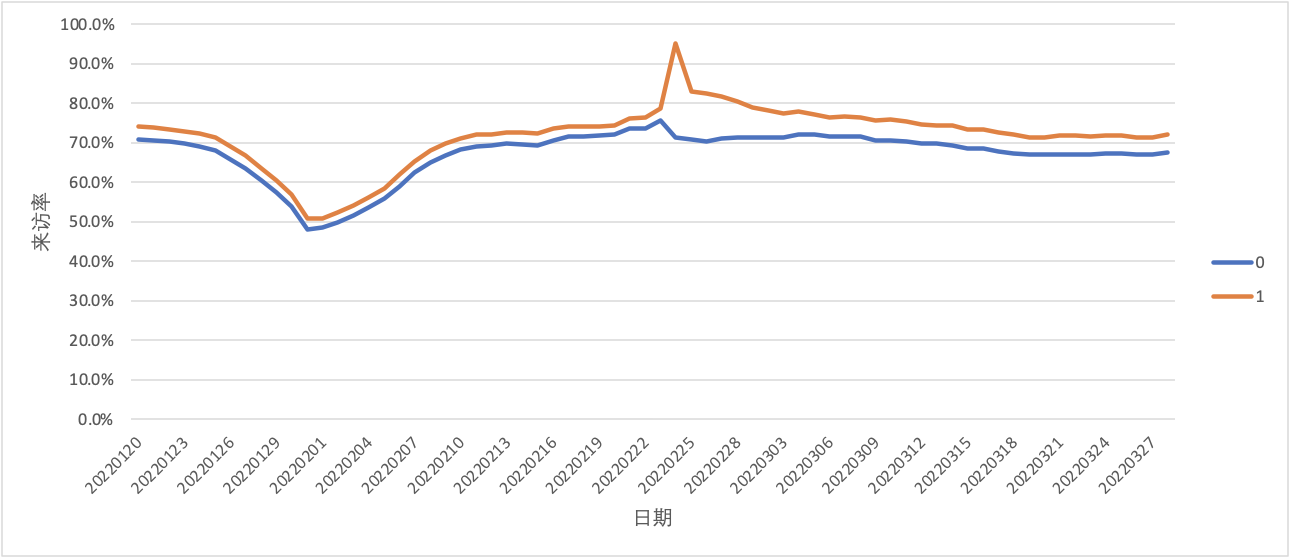
增量计算
因为满足平行趋势假设,我们可以用双重差分法(DID)去计算干预带来的增量;需注意的是,计算实验组与对照组的差异时,我们通常需要取一段时间的均值,避免波动带来的影响。
最终得到的结论类似于:用户在购买商品后,能够给来访率带来1.5%(30天日均)的提升。
其他情况
在一些情况下,也会有其他结果的出现。
- 无显著增量
用户在干预之后来访率有一个短暂的提升,但随着时间的推移两组用户趋于一致。这种情况下我们通常认为干预并没有给用户来访带来显著的提升。为了识别出这种情况,我们也可以通过假设检验或计算差值中位数的方式进行验证。
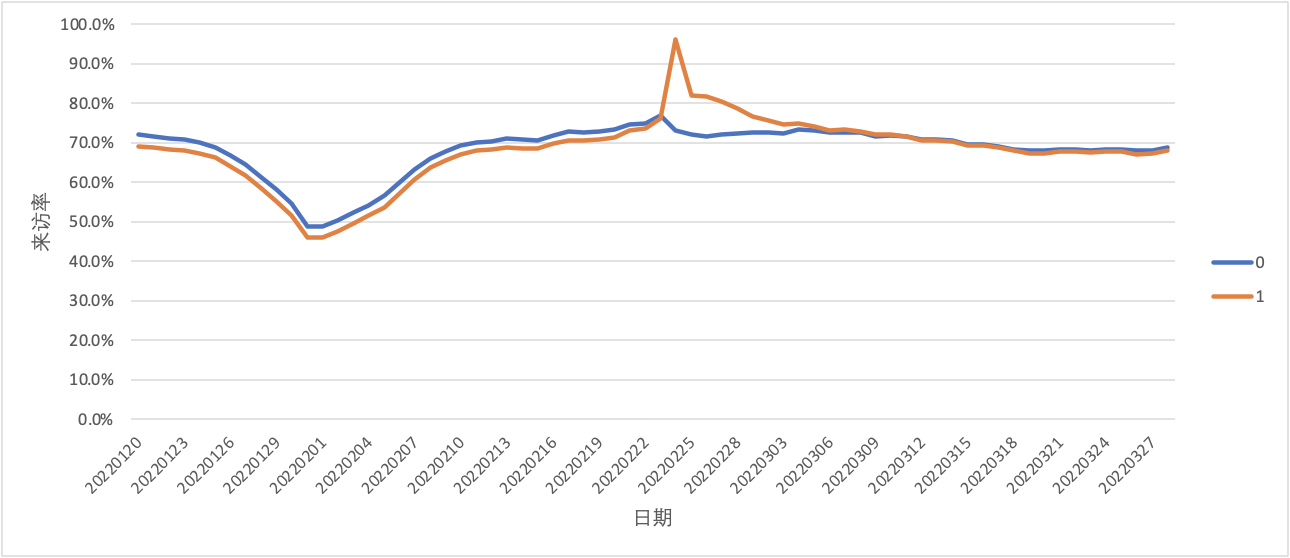
- 不满足平行趋势假设
从下图可以看到,左侧区域实验组与对照组的趋势不一致(不平行),这代表我们前面完成的匹配质量较差,需要优化匹配模型。对于平行趋势的检验,除了图示法(肉眼看是否平行)我们也可以通过T检验的方式来验证。
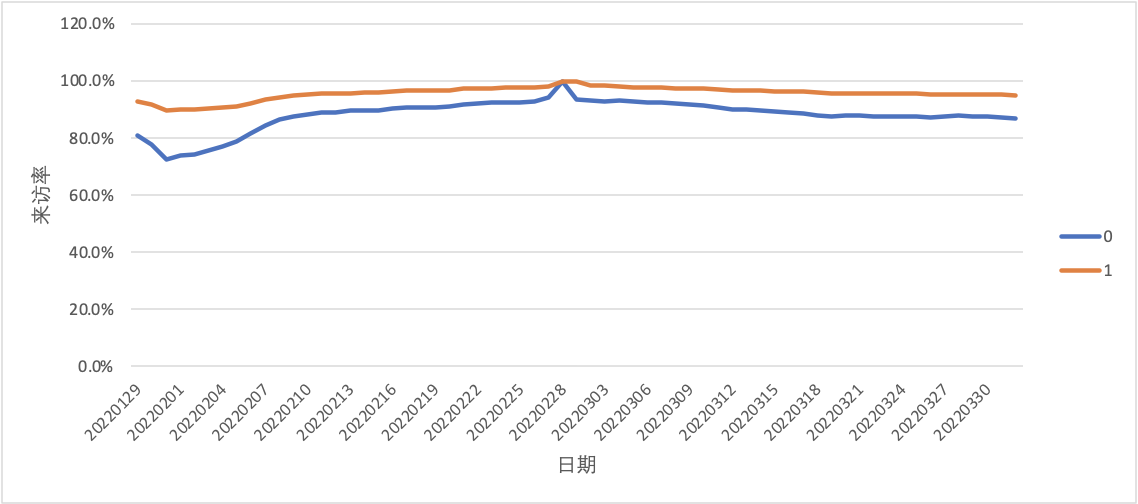
其他值得一提的点
ATT与ATE的区别
- ATE:average treatment effect
- ATT:average treatment effect on the treated
可以认为ATE是人群整体的干预增量效果,而ATT是实际被干预人群的干预增量效果。通常我们通过PSM+DID计算的是ATT,因为ATE还会涉及人群的干预率。更详细的解释可以参考stackexchange上的这个回答:https://stats.stackexchange.com/questions/308397/why-is-average-treatment-effect-different-from-average-treatment-effect-on-the-t
Bias与Variance
在匹配算法的步骤,我们有提到bias与varianc:
- Bias 偏差:期望预测与真实结果之间的偏离程度,刻画算法本身的拟合能力
- Variance 方差:同样大小训练集的变动所导致的学习性能变化,刻画数据扰动所造成的影响
可以认为bias代表算法本身的拟合能力而variance代表算法的稳定性,在匹配的不同方法中它们也存在trade-offs:
算法 | Bias | Variance |
NN+多邻居 | + | - |
NN+最近邻 | - | + |
+边界值 | - | + |
无边界值 | + | - |
有放回 | - | + |
无放回 | + | - |
敏感性测试 Sensitivity Analysis
在前置知识介绍的部分有提到,做PSM需要满足两个假设——条件独立和共支撑。
对于第一个条件,其含义便是我们需要观测到所有同时影响到treatment和outcome的特征,否则估算的ATT会存在偏差。对于common support,我们实际上计算的是倾向得分重叠区域的ATT,其实际上也可能是有偏的。在这种情况下,我们需要去进行sensitivity analysis。换句话说,我们计算得到的增量结果其实是不稳健的,我们可以通过纳入不确定性的来估算一个ATT的区间,使之稳定性得到提升。
总结
在文章的最后,我们对PSM的整体流程进行一个梳理(可以看到真的不复杂),同时对PSM的优点与缺点进行简单的介绍。
完整流程
- 选择同时影响treatment与outcome的特征,基于特征对treatment进行二分类建模,得到倾向分;
- 在支撑集上,基于重要特征与倾向分进行匹配,为被干预用户找到匹配的样本;
- 对匹配结果的质量进行检验,检验通过的话进入下一步,否则返回第二步进行匹配的优化;
- 基于匹配的结果进行平行趋势验证,验证通过后通过双重差分法进行增量计算。
PSM的优缺点
- 优点
- 在无法进行随机试验的情况下,可构建虚拟的对照组并对增量进行可信的估算;
- 实现较为容易,实验组的样本能够充分的利用。
- 缺点
- PSM最主要的一个缺点是——使用者永远无法保证所有的混淆变量都被包含在建模用的特征当中;
- 但可通过敏感性分析校验:如增减混淆变量后重复完成计算步骤观测结果是否一致,或通过纳入不确定性对估算增量的区间值
- 当支撑集(实验、对照组的倾向分交集)较小时,PSM+DID估计的局部样本的增量,可能无法代表整体。
整体来说,若不过分追求准确性,PSM+DID是一个对因果增量预估的较为靠谱的方式。当实现过程中存在卡点或假设无法满足时,除了优化模型还可以尝试看看逆概率加权和合成控制法等其他方法。






